【优化调度】基于改进遗传算法求解农业水资源调度问题(Matlab代码实现)
- 2026-02-09 03:05:06
💥💥💞💞欢迎来到本博客❤️❤️💥💥
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
💥1 概述
科学的渠系配水决策可以减少渠系输水过程中的渗水损失和无效弃水,提高灌溉水利用率。国内外学者对渠系优化配水决策方法进行了许多研究,Suryavanshi等(1986)最早在假定上级配水渠道是由一组等流量流管组成,流管流量等于下级渠道流量的基础上,以减小渠道工程投资为目标,确定上级渠道流管数的1992)将其用于渠系优化配水研究中,提出了基于0一线性规划配水模型及算法["。基于上述思想﹐王智等(l规划法的下级渠道等流量时优化配水模型并编制了计算机程序2。Reddy等(1999) [3'、Anwar等(2001)对文献[1]、[2]的配水模型进行了改进,加入了各下级渠道在用户预定的配水时间窗内配水的要求,解决了轮期内下级渠道配水时间与实际需求配水时间差异而造成的作物减产问题。而吕宏兴等(2000)改进了文献[2]模型的目标函数,提出了各下级渠道配水时间均一化处理方法,使上级渠道可在同一时间关闭.减少了配水闸门调节次数IS'。骆莉等(2000)、宋松柏等(2004)分别研究了文献[2]、[5]模型的遗传算法求解方法,显著提高了模型的求解速度﹐解决了在下级渠道较多时模型求解困难的问题5.1。马孝义等(2005)以渠系输水损失最小为目标,提出了以灌水组数最大和最长灌水组配水时问最小的二级目标优化配水模型及遗传算法求解方法,并在对复杂渠系抽象概化的基础上﹐研制了一种易于快速搭建、通用性强的渠系配水软件[3]。但上述研究都是基于流管假定下的改进,只能解决下级渠道流量相等条件下的渠系优化配水编组问题。而在大多数情况下﹐由于地形、作物种植类型的变化等,下级渠道设计流量变化较大,现有方法存在明显缺陷。为此,需进一步研究下级渠道流量不等时的渠系优化配水模型及其求解算法。
农业水资源调度问题是一个复杂的优化问题,涉及到资源分配、灌溉管理等方面。利用改进遗传算法(GA)来求解这一问题是一个很好的选择,因为遗传算法擅长处理复杂的优化问题,并且能够在搜索空间中找到全局最优解或者接近最优解。
基于改进遗传算法求解农业水资源调度问题研究
一、引言
水是生命之源、生产之要、生态之基。目前全球水资源短缺问题日益严峻,据估测到 2025 年全球约有 23 亿人口将会面临水资源短缺问题。农业作为用水大户,其水资源的合理调度对于缓解水资源危机、实现可持续发展至关重要。
水资源调度管理旨在实现水资源的优化配置,保障生产生活和生态合理用水需求。其管理对象涵盖流域内各区域地表水、地下水和非传统水源。在调度类型方面,根据调度时间和紧迫性可分为常规水资源调度和应急水资源调度;按照目的可分为防汛抗旱应急调度、生态用水调度、供水调度等;根据调度影响区域可分为流域内调度和跨流域调度。
近些年来,智能优化算法在水资源优化调度领域得到广泛应用。刘攀等人提出遗传算法在水库调度中的应用,解决了时效性要求不高的实时调度问题和水库规划设计问题;张忠波等人提出改进遗传算法,利用 GA 双层收敛方法和较强的鲁棒性,提高了全局搜索能力;昌易等人提出基于遗传算法的区域水资源调度,建立涵盖社会效益、经济效益和环境效益的模型,实现了水资源的可持续发展;黄显峰等人提出多目标混沌遗传算法,解决了要求目标函数和约束条件连续、可微的困难。然而,这些算法在水资源调度过程中仍然存在收敛速度慢、易陷入局部优化等问题。本文引入改进遗传算法,旨在提高农业水资源调度的综合效益。
二、相关理论基础
(一)农业水资源调度问题分析
农业水资源调度涉及到众多因素,包括不同农作物的需水量、灌溉时间要求、水资源的可获取量(如河流流量、地下水位等)、灌溉设施的输水能力以及不同区域的用水优先级等。这些因素相互交织,使得农业水资源调度成为一个复杂的多约束、多目标优化问题。
在实际情况中,由于地形、作物种植类型的变化等,下级渠道设计流量变化较大,这进一步增加了调度的难度。例如,在山区和平原地区,灌溉方式和水资源的分布与利用方式有很大差异;不同作物在不同生长阶段对水分的需求也各不相同。
(二)遗传算法原理
遗传算法(Genetic Algorithm,GA)是一种基于自然选择和遗传变异的优化算法。它通过模拟生物进化过程,在解空间中搜索最优解。其基本操作包括编码、种群初始化、选择、交叉和变异。
编码是将问题的解表示为遗传算法能够处理的染色体形式,常见的编码方式有二进制编码、实数编码等。种群初始化是随机生成一组初始染色体,构成初始种群。选择操作根据个体的适应度值选择优良个体,适应度值越高的个体被选择的概率越大。交叉操作是将优良个体的染色体进行交换,生成新的个体,从而继承父代的优良基因。变异操作则是对染色体上的某些基因进行随机变异,以增加种群的多样性,避免陷入局部最优解。
(三)传统遗传算法在农业水资源调度中的局限性
- 收敛速度慢
:在处理复杂的农业水资源调度问题时,传统遗传算法可能需要大量的迭代次数才能收敛到较优解,这导致求解效率低下,无法满足实际应用中的实时性要求。 - 易陷入局部优化
:由于遗传算法的搜索过程受到初始种群和操作参数的影响较大,在搜索过程中容易陷入局部最优解,无法找到全局最优解,从而导致水资源调度方案不是最优的,不能充分发挥水资源的利用效率。
三、改进遗传算法设计
(一)改进策略
为克服传统遗传算法的局限性,本文提出以下改进策略:
- 初始化种群优化
:采用基于问题先验知识的初始化方法,结合农业水资源调度的实际情况,生成更具代表性和多样性的初始种群。例如,根据不同区域的作物种植面积、需水规律等信息,合理分配初始染色体上的基因值,使初始种群更接近问题的最优解,从而加快算法的收敛速度。 - 自适应交叉和变异算子
:传统遗传算法的交叉和变异概率通常是固定的,这在不同的优化阶段可能无法达到最佳效果。本文采用自适应交叉和变异算子,根据种群的进化情况动态调整交叉和变异概率。在算法初期,为了保持种群的多样性,提高交叉和变异概率,以便在更大的解空间中搜索;在算法后期,为了避免破坏优良个体,降低交叉和变异概率,使算法能够更快地收敛到最优解。具体实现方式可以根据种群的平均适应度值和最优适应度值的差异来调整交叉和变异概率。 - 引入精英保留策略
:精英保留策略是指在每一代进化过程中,直接保留上一代中的最优个体,使其不参与遗传操作,直接进入下一代种群。这样可以保证最优解不会因为遗传操作而丢失,确保算法能够收敛到全局最优解。
(二)改进遗传算法流程
- 输入参数初始化
:确定算法的基本参数,如种群规模、最大迭代次数、初始交叉概率、初始变异概率等,并输入农业水资源调度问题的相关数据,如农作物需水量、水资源量、灌溉设施参数等。 - 种群初始化
:根据改进的初始化方法,生成初始种群。 - 计算适应度值
:根据农业水资源调度问题的目标函数(如水资源利用效率最大化、灌溉成本最小化等),计算每个个体的适应度值。 - 选择操作
:采用轮盘赌选择法或锦标赛选择法等,根据个体的适应度值选择优良个体。 - 交叉操作
:按照自适应交叉概率,对选择的优良个体进行交叉操作,生成新的个体。 - 变异操作
:按照自适应变异概率,对新生成的个体进行变异操作。 - 精英保留
:保留上一代中的最优个体,将其加入到新一代种群中。 - 判断终止条件
:检查是否达到最大迭代次数或满足其他终止条件(如最优解连续多代不变等)。如果满足终止条件,则输出最优解;否则,返回步骤 3 继续迭代。
四、基于改进遗传算法的农业水资源调度模型构建
(一)目标函数
农业水资源调度的目标通常是多方面的,本文综合考虑水资源利用效率、灌溉成本和作物产量等因素,构建如下多目标函数:
 编辑
编辑
 编辑
编辑
(二)约束条件
- 水资源总量约束
:
 编辑
编辑
五、实验验证与结果分析
以运行结果为准。
(一)实验数据准备
以某地区的农业灌溉系统为例,收集该地区的农作物种植信息(包括作物种类、种植面积等)、水资源信息(河流流量、地下水位等)、灌溉设施参数(渠道输水能力、泵站扬程等)以及不同作物的需水规律等数据,作为实验的输入数据。
(二)实验设置
分别采用传统遗传算法和改进遗传算法对农业水资源调度问题进行求解。设置种群规模为 50,最大迭代次数为 200,传统遗传算法的交叉概率为 0.8,变异概率为 0.05。改进遗传算法采用自适应交叉和变异算子,初始交叉概率为 0.9,初始变异概率为 0.1。每个算法运行 10 次,记录每次运行的结果。
(三)实验结果对比与分析
- 收敛速度对比
:从迭代过程的收敛曲线可以看出,改进遗传算法在迭代初期就能快速向最优解靠近,收敛速度明显快于传统遗传算法。传统遗传算法需要较多的迭代次数才能达到较优解,且在收敛过程中容易出现波动。 - 最优解质量对比
:在 10 次运行中,改进遗传算法得到的最优解的平均适应度值明显高于传统遗传算法。这表明改进遗传算法能够更有效地搜索到全局最优解,提高了农业水资源调度的综合效益。 - 稳定性对比
:改进遗传算法的运行结果相对更加稳定,每次运行得到的最优解之间的差异较小;而传统遗传算法的结果波动较大,说明改进遗传算法具有更好的鲁棒性。
六、结论与展望
(一)研究结论
本文针对传统遗传算法在农业水资源调度中存在的收敛速度慢、易陷入局部优化等问题,提出了一种改进遗传算法。通过优化初始化种群、采用自适应交叉和变异算子以及引入精英保留策略等方法,提高了算法的性能。实验结果表明,改进遗传算法在收敛速度、最优解质量和稳定性方面均优于传统遗传算法,能够为农业水资源调度提供更优的方案,提高水资源的利用效率,降低灌溉成本,增加作物产量。
(二)研究展望
进一步考虑农业水资源调度中的不确定性因素,如气候变化对水资源量和农作物需水量的影响,将不确定性分析方法与改进遗传算法相结合,使调度方案更具适应性和可靠性。 探索将改进遗传算法与其他智能算法(如粒子群算法、蚁群算法等)进行融合,形成更高效的混合优化算法,以解决更复杂的农业水资源调度问题。 开展实际应用研究,将本文提出的方法应用于更多地区的农业灌溉系统中,通过实际数据验证和完善算法,为农业水资源的科学管理和可持续利用提供有力支持。
📚2 运行结果
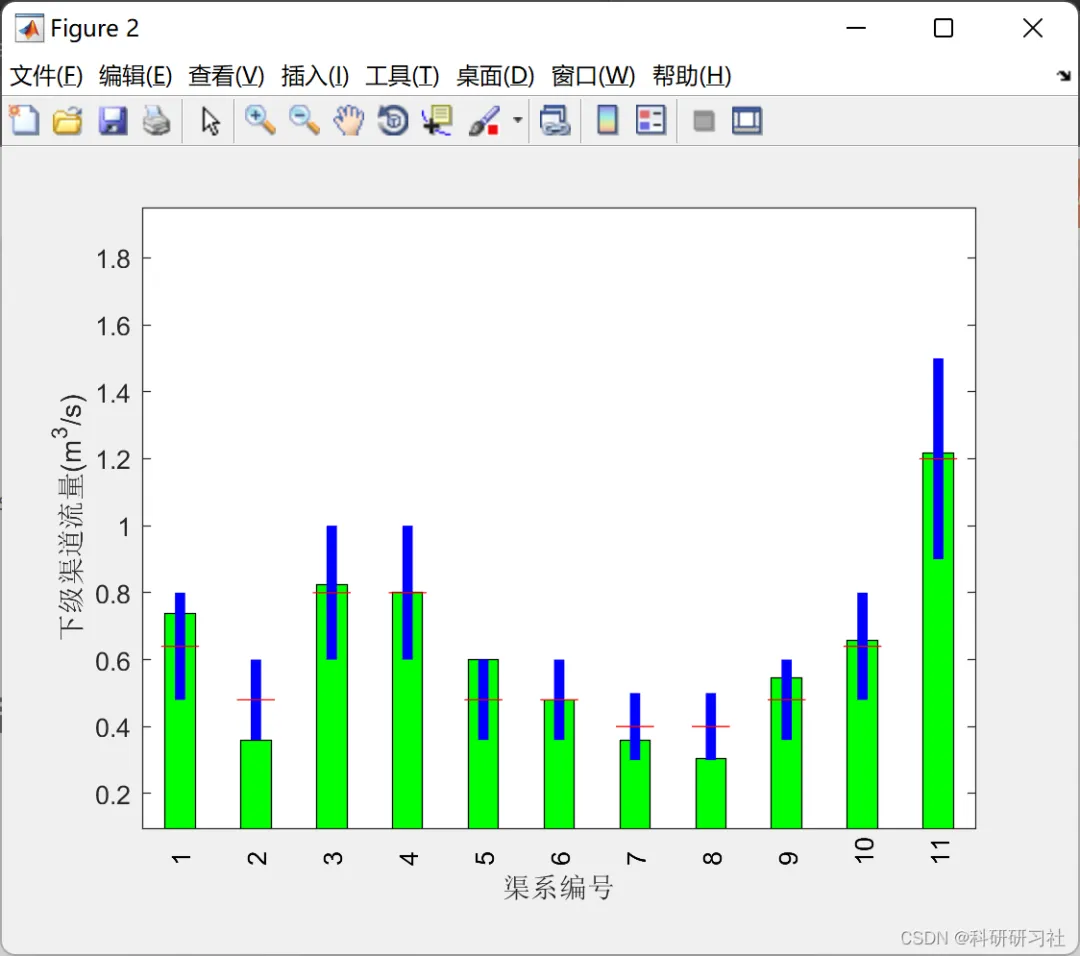 编辑
编辑
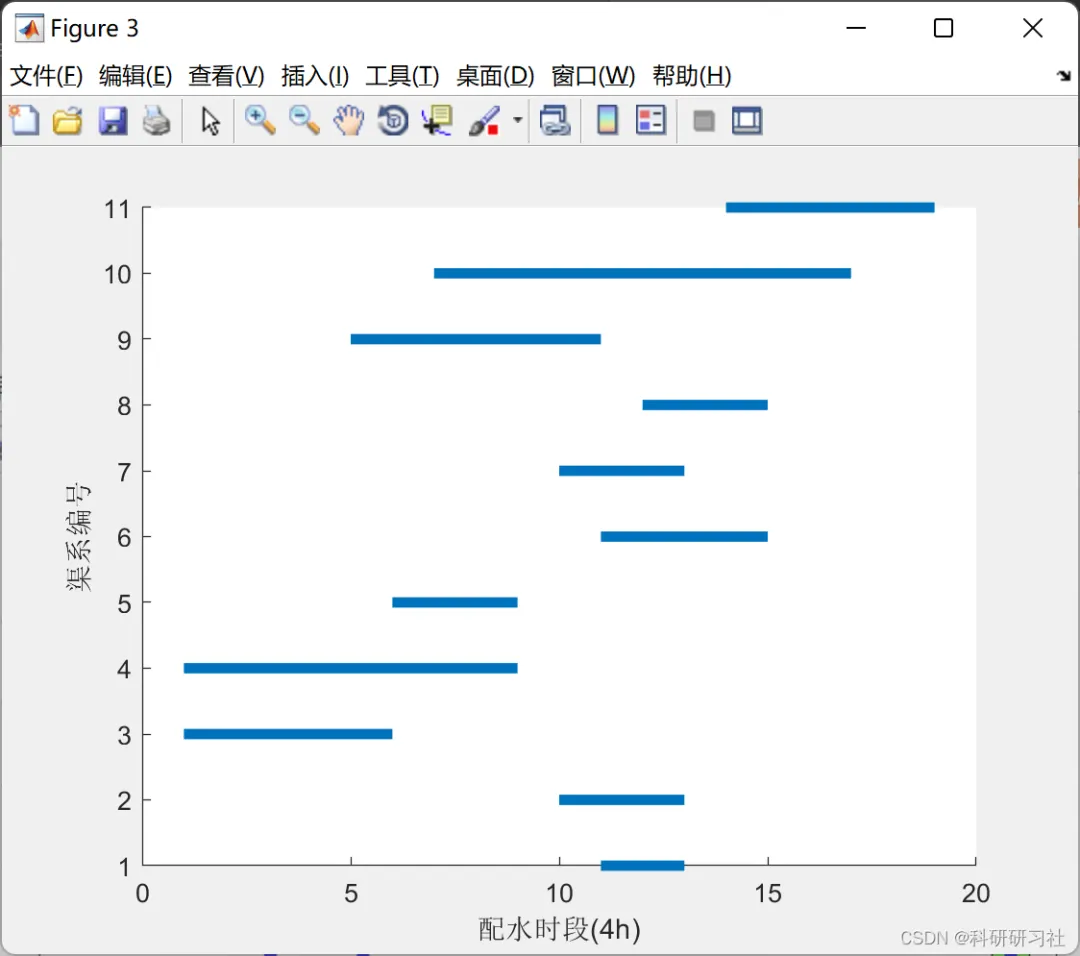 编辑
编辑
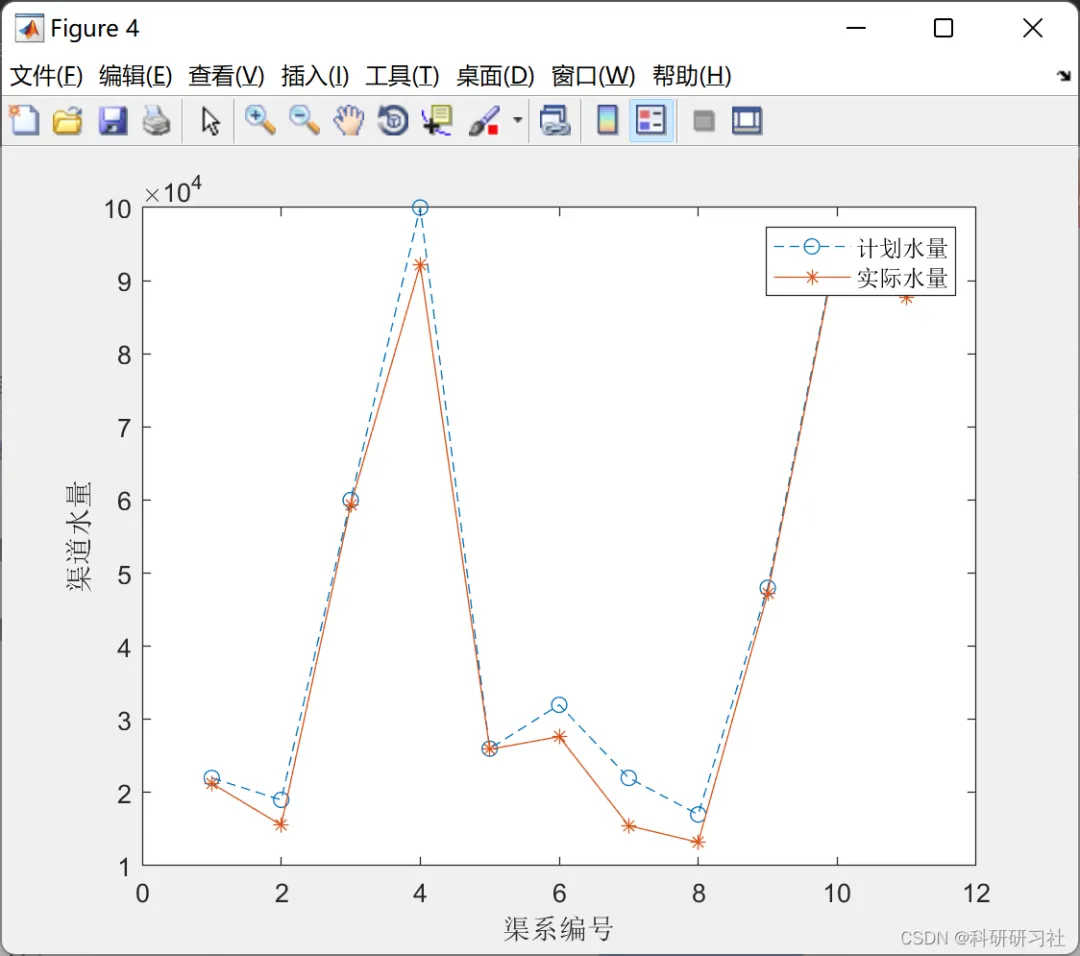 编辑
编辑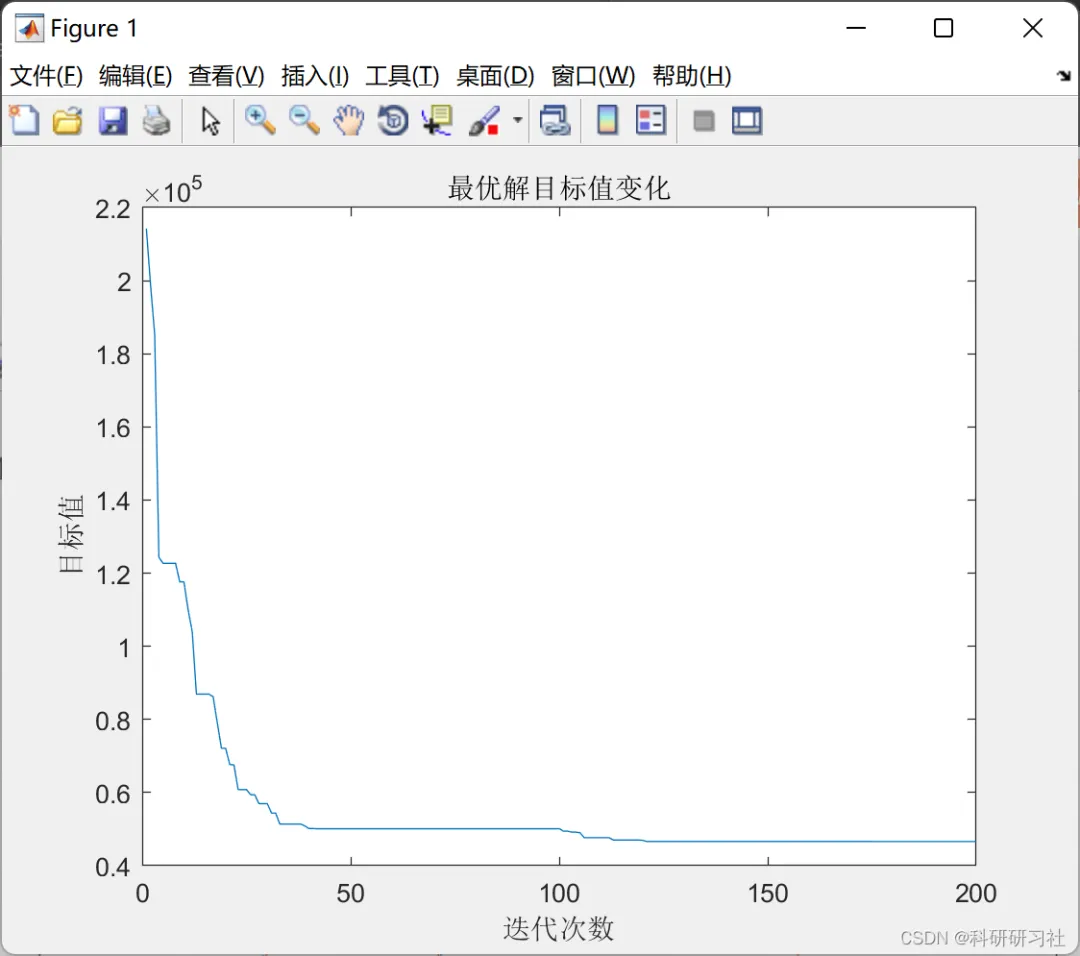 编辑
编辑
部分代码:
function offspring=Mutate(population,state)% 本函数完成变异操作global T Qmax QminN=length(population);
if state<0.5 offspring1 = population; for i=1:N pop1 = population(i); pop2 = population(randperm(N,1)); % 随机挑选1-2个位置进行交叉操作 pos = randperm(11,randi([1,3],1)); pop1.tstart(pos) = pop2.tstart(pos); pop1.tend(pos) = pop2.tend(pos); pop1.q(pos) = pop2.q(pos); offspring1(i) = pop1; end offspring2 = population; for i=1:N pop1 = population(i); % 开始时间 pos = randperm(11,randi([1,2],1)); pop1.tstart(pos) = pop1.tstart(pos) + randi([-2,2],size(pos)); pop1.tstart(pos) = max(pop1.tstart(pos),1); pop1.tstart(pos) = min(pop1.tstart(pos),T*24/4-1); %修复上下界 pop1.tend(pos) = max(pop1.tstart(pos),pop1.tend(pos)); offspring2(i) = pop1; end offspring3 = population; for i=1:N pop1 = population(i); % 结束时间 pos = randperm(11,randi([1,2],1)); pop1.tend(pos) = pop1.tend(pos) + randi([-2,2],size(pos)); pop1.tend(pos) = max(pop1.tstart(pos),pop1.tend(pos)); pop1.tend(pos) = min(pop1.tstart(pos),T*24/4); %修复上下界 offspring3(i) = pop1; end offspring = CalObj([offspring1,offspring2,offspring3]);else offspring4 = population; for i=1:N pop1 = population(i); % 供水量 pos = randperm(11,randi([1,2],1)); pop1.q(pos) = pop1.q(pos) + 0.2.*rands(1,length(pos)); pop1.q = max(Qmin,pop1.q); pop1.q = min(Qmax,pop1.q); %修复上下界 offspring4(i) = pop1; end offspring = CalObj(offspring4);end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.[3]赵小强,何智娥.基于改进混沌遗传算法的水资源优化调度[J].兰州理工大学学报. 2015,41(04)
🌈4 Matlab代码实现
公众号后台回复:程序下载
